DICAS
Por Camilo Filho*
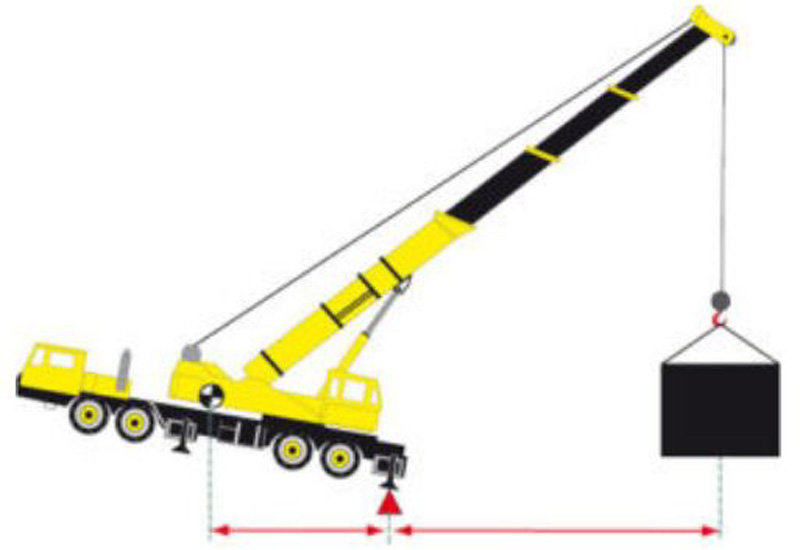
Um guindaste móvel é projetado tendo em conta os princípios de momento (alavanca) e equilíbrio. Simplificando, um guindaste deve ser capaz de içar cargas, através do uso do princípio da alavanca, mantendo seu equilíbrio.
Antes de nos aprofundarmos nesses conceitos, precisamos falar sobre a força da gravidade. Sabemos por Newton e Einstein que o fenômeno natural da gravidade está presente. Bem, se houver dúvida em relação a isso, simplesmente deixe uma manilha de 1” cair de uma altura de 1,0 m no seu pé, que rapidamente você comprovará que ela está aí. No içamento de cargas, a posição do Centro de Gravidade (ou CG) de uma carga, é fundamental para o sucesso da operação. O “símbolo o do centro de gravidade”, nas ilustrações abaixo, é usado para mostrar o local onde está localizado o CG de um objeto. O CG de qualquer objeto é considerado o ponto no objeto onde o peso está distribuído uniformemente. Também o C.G. é considerado o ponto onde toda a massa do corpo está ali concentrada.
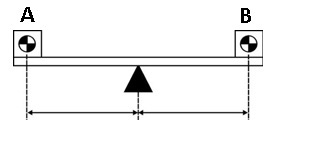
Agora, imaginemos uma gangorra (adiante veremos que é exatamente como trabalha um guindaste). A gangorra permanece em equilíbrio enquanto o momento proporcionado pelos dois pesos A e B for igual. Se os pesos colocados na gangorra fossem diferentes, esta inclinaria na direção do lado mais pesado, haja vista que as distâncias das cargas ao ponto de apoio são iguais. Se aumentarmos o peso do lado A, a única maneira de manter o equilíbrio é mover o ponto de apoio para mais perto do objeto mais pesado, conforme mostrado abaixo. Ao mover o apoio, cada contrapeso equilibra o outro e a gangorra permanece em equilíbrio.
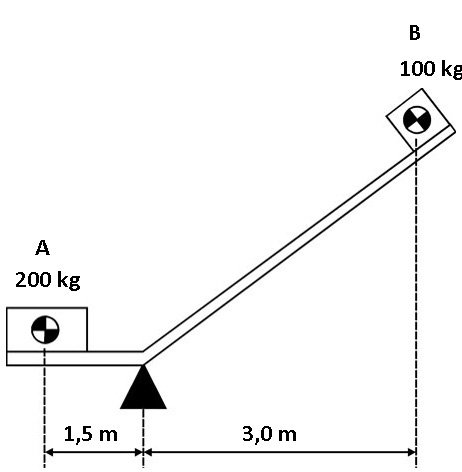
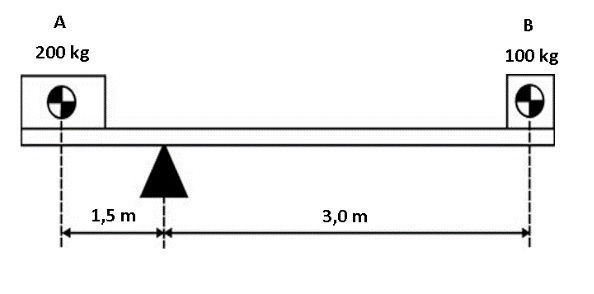
O balanceamento depende do momento exercido por cada carga. O momento é o resultado da multiplicação do peso de um objeto, pela distância que o objeto se encontra do ponto de apoio. Na ilustração abaixo, a carga de 200 kg é multiplicada pela distância que a carga se encontra do ponto de apoio (1,5 m). O peso de 100 kg é multiplicado pela sua distância ao apoio (3,0 m). Se os dois lados da equação são iguais, o sistema permanece em equilíbrio. A matemática é bastante simples. Você multiplica os 200 kg vezes 1,5 m, o que equivale a 300 kg.m. Em seguida, multiplique o peso de 100 kg vezes sua distância ao apoio. O resultado de 300 kgm mostra que os momentos são iguais, ou que a alavanca provocada pelas cargas em ambos os lados é igual.
 Podemos aplicar esse conceito para os guindastes, de forma que, na ilustração abaixo, à direita do apoio é levantada, de modo parecido com a lança de um guindaste. Desde que o momento ou alavanca exercido por cada carga permaneça igual, o sistema permanecerá em equilíbrio
Podemos aplicar esse conceito para os guindastes, de forma que, na ilustração abaixo, à direita do apoio é levantada, de modo parecido com a lança de um guindaste. Desde que o momento ou alavanca exercido por cada carga permaneça igual, o sistema permanecerá em equilíbrio
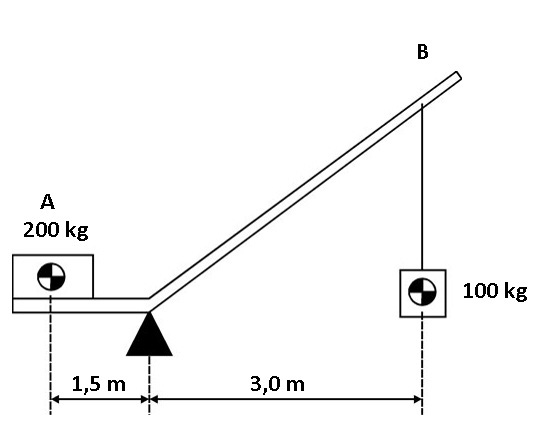
Agora vejamos o que acontece quando, ao invés da carga estar apoiada, ela está suspensa, abaixo do seu ponto de apoio, como na lança de um guindaste. Pela figura abaixo, vemos que o sistema continua em equilíbrio, desde que os momentos permaneçam iguais, importando apenas a linha de aplicação das forças peso. Este exemplo é ótimo, contanto que não haja mudança de configuração nem da carga nem da distância; mas sabemos que, no trabalho do guindaste, isso não acontece: o trabalho é dinâmico. Içamos vários tipos de cargas com pesos variáveis, mudamos a distância, subindo/baixando lança ou estendendo/retraindo o telescópico. Além do que, este tipo de equilíbrio, em que os dois lados estão iguais, é chamado de equilíbrio instável, onde qualquer variação, por menor que seja, incluindo aí até uma pequena rajada de vento, pode desbalancear o sistema e provocar, no caso do guindaste, seu tombamento
Estes exemplos mostram como o equilíbrio é definido. Sabemos que um guindaste deve ser capaz de se manter em equilíbrio sob uma variedade de alterações de carga, mudanças de raio e outros fatores que influenciam o equilíbrio. No campo, pensamos em equilíbrio como “estabilidade” – e a capacidade de um guindaste ficar estável e realizar sua tarefa com segurança é o objetivo final.
LEIA MAIS DICAS DO CAMILO SOBRE IÇAMENTOS DE CARGAS